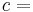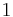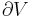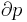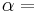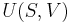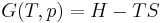Real gas

Thermodynamics
Systems
State:
Equation of state
Ideal gas · Real gas
Phase of matter · Equilibrium
Control volume · Instruments
Processes:
Isobaric · Isochoric · Isothermal
Adiabatic · Isentropic · Isenthalpic
Quasistatic · Polytropic
Free expansion
Reversibility · Irreversibility
Endoreversibility
Cycles:
Heat engines · Heat pumps
Thermal efficiency

Real gases – as opposed to a perfect or ideal gas – exhibit properties that cannot be explained entirely using the ideal gas law. To understand the behaviour of real gases, the following must be taken into account:

For most applications, such a detailed analysis is unnecessary, and the ideal gas approximation can be used with reasonable accuracy. On the other hand, real-gas models have to be used near the condensation point of gases, near critical points, at very high pressures, and in other less usual cases.

Contents

Models

Main article: Equation of state

van der Waals model

Main article: van der Waals equation

Real gases are often modeled by taking into account their molar weight and molar volume

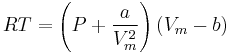
RT=\left(P%2B\frac{a}{V_m^2}\right)(V_m-b)

Where P is the pressure, T is the temperature, R the ideal gas constant, and Vm the molar volume. a and b are parameters that are determined empirically for each gas, but are sometimes estimated from their critical temperature (Tc) and critical pressure (Pc) using these relations:

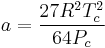
a=\frac{27R^2T_c^2}{64P_c}

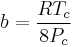
b=\frac{RT_c}{8P_c}

Redlich–Kwong model

The Redlich–Kwong equation is another two-parameters equation that is used to model real gases. It is almost always more accurate than the van der Waals equation, and often more accurate than some equations with more than two parameters. The equation is

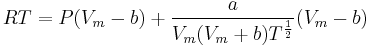
RT=P(V_m-b)%2B\frac{a}{V_m(V_m%2Bb)T^\frac{1}{2}}(V_m-b)

where a and b two empirical parameters that are not the same parameters as in the van der Waals equation. These parameters can be determined:

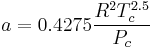
a=0.4275\frac{R^2T_c^{2.5}}{P_c}

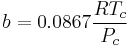
b=0.0867\frac{RT_c}{P_c}

Berthelot and modified Berthelot model

The Berthelot equation (named after D. Berthelot[1] is very rarely used,

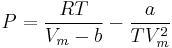
P=\frac{RT}{V_m-b}-\frac{a}{TV_m^2}

but the modified version is somewhat more accurate

P=\frac{RT}{V_m}\left[1%2B\frac{9P/P_c}{128T/T_c}\left(1-\frac{6}{(T/T_c)^2}\right)\right]

Dieterici model

This model (named after C. Dieterici[2]) fell out of usage in recent years

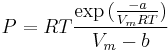P=RT\frac{\exp{(\frac{-a}{V_mRT})}}{V_m-b}.

Clausius model

The Clausius equation (named after Rudolf Clausius) is a very simple three-parameter equation used to model gases.

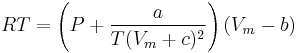
RT=\left(P%2B\frac{a}{T(V_m%2Bc)^2}\right)(V_m-b)

where

a=\frac{27R^2T_c^3}{64P_c}

b=V_c-\frac{RT_c}{4P_c}

c=\frac{3RT_c}{8P_c}-V_c

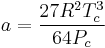
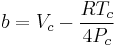
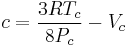
where Vc is critical volume.

Virial model

The Virial equation derives from a perturbative treatment of statistical mechanics.

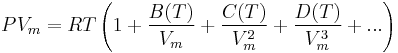
PV_m=RT\left(1%2B\frac{B(T)}{V_m}%2B\frac{C(T)}{V_m^2}%2B\frac{D(T)}{V_m^3}%2B...\right)

or alternatively

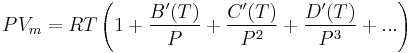
PV_m=RT\left(1%2B\frac{B^\prime(T)}{P}%2B\frac{C^\prime(T)}{P^2}%2B\frac{D^\prime(T)}{P^3}%2B...\right)

where A, B, C, A′, B′, and C′ are temperature dependent constants.

Peng–Robinson model

This two parameter equation (named after D.-Y. Peng and D. B. Robinson[3]) has the interesting property being useful in modeling some liquids as well as real gases.

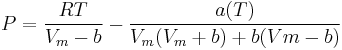
P=\frac{RT}{V_m-b}-\frac{a(T)}{V_m(V_m%2Bb)%2Bb(Vm-b)}

Wohl model

The Wohl equation (named after A. Wohl[4]) is formulated in terms of critical values, making it useful when real gas constants are not available.

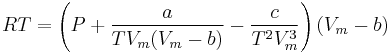
RT=\left(P%2B\frac{a}{TV_m(V_m-b)}-\frac{c}{T^2V_m^3}\right)(V_m-b)

where

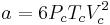
a=6P_cT_cV_c^2

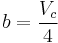
b=\frac{V_c}{4}

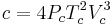c=4P_cT_c^2V_c^3.

Beattie–Bridgeman model

The Beattie–Bridgeman equation (named after James A. Beattie and Oscar C. Bridgeman[5])

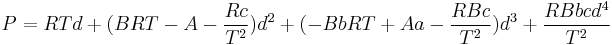
P=RTd%2B(BRT-A-\frac{Rc}{T^2})d^2%2B(-BbRT%2BAa-\frac{RBc}{T^2})d^3%2B\frac{RBbcd^4}{T^2}

where d is the molal density and a, b, c, A, and B are empirical parameters.

Benedict–Webb–Rubin model

Main article: Benedict–Webb–Rubin equation

The BWR equation, sometimes referred to as the BWRS equation,

P=RTd%2Bd^2\left(RT(B%2Bbd)-(A%2Bad-a{\alpha}d^4)-\frac{1}{T^2}[C-cd(1%2B{\gamma}d^2)\exp(-{\gamma}d^2)]\right)

where d is the molal density and where a, b, c, A, B, C, α, and γ are empirical constants.

See also

References

  1. ^ D. Berthelot in Travaux et Mémoires du Bureau international des Poids et Mesures – Tome XIII (Paris: Gauthier-Villars, 1907)
  2. ^ C. Dieterici, Ann. Phys. Chem. Wiedemanns Ann. 69, 685 (1899)
  3. ^ D.-Y. Peng and D.B. Robinson, "A New Two-Constant Equaiton of State," Ind. Eng. Chem. Fund., 15, 59 (1976)
  4. ^ A. Wohl "Investigation of the condition equation", Zeitschrift für Physikalische Chemie (Leipzig) 87 pp. 1–39 (1914)
  5. ^ James A. Beattie and Oscar C. Bridgeman "A NEW EQUATION OF STATE FOR FLUIDS. I. APPLICATION TO GASEOUS ETHYL ETHER AND CARBON DIOXIDE", Journal of the American Chemical Society 49 pp. 1665 – 1667 (1927)

External links